0843

843. n-皇后问题

题目

$n-$皇后问题是指将 $n$ 个皇后放在 $n \times n$ 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

现在给定整数 $n$，请你输出所有的满足条件的棋子摆法。

输入格式

共一行，包含整数 $n$。

输出格式

每个解决方案占 $n$ 行，每行输出一个长度为 $n$ 的字符串，用来表示完整的棋盘状态。

其中 . 表示某一个位置的方格状态为空， Q 表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

注意：行末不能有多余空格。

输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围

$1 \le n \le 9$

输入样例：

4

输出样例：

.Q..
...Q
Q...
..Q.

..Q.
Q...
...Q
.Q..

题解

前置题目：0842

前置知识：数学

本题知识：搜索与图论-DFS

题目分析

使用dfs

• 第一种搜索顺序，按行枚举，每行枚举一个
• 第二种搜索顺序，按个枚举，枚举n^2次，每个位置都判断两次是否能成为皇后

剪枝：如果这一行没有皇后&&这一列没有皇后&&主对角线没有皇后&&副对角线没有皇后，那么就是合法的位置，否则直接返回。

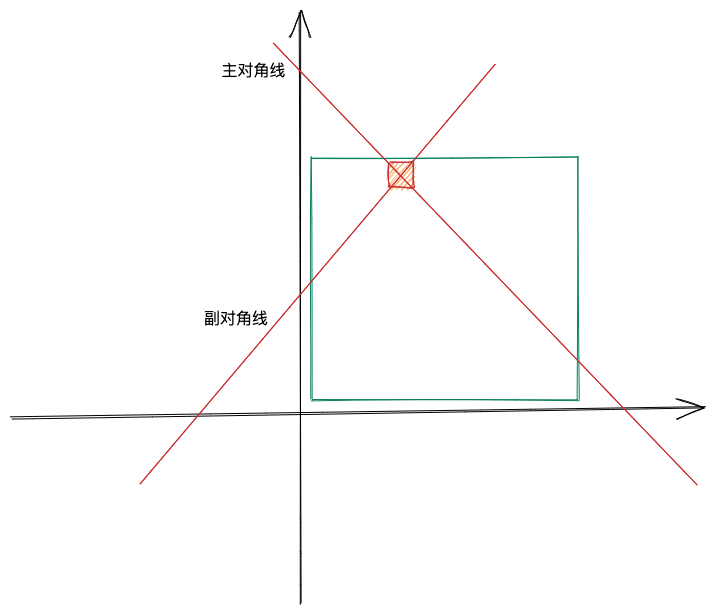
如何确定主对角线和副对角线的下标位置？

n: 输入

i: 第几列

u: 从0开始递归，递归到第几个

模拟一个坐标轴，当前所在位置就在(i, n-u)

主对角线：y = -x + b

b = x + y = i - u + n = 下标位置

副对角线：y = x + b, 但如图 n - b 才下标位置

b = y - x = n - u - i

n - b = n - (n - u - i) = i +u = 下标位置

具体下标位置数组是否从0开始不重要，只要保证前后查找的一致性和数组不越界即可