给定一个
矩阵中第
一个人从滑雪场中的某个区域内出发,每次可以向上下左右任意一个方向滑动一个单位距离。
当然,一个人能够滑动到某相邻区域的前提是该区域的高度低于自己目前所在区域的高度。
下面给出一个矩阵作为例子:
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
在给定矩阵中,一条可行的滑行轨迹为
在给定矩阵中,最长的滑行轨迹为
现在给定你一个二维矩阵表示滑雪场各区域的高度,请你找出在该滑雪场中能够完成的最长滑雪轨迹,并输出其长度(可经过最大区域数)。
第一行包含两个整数
接下来
输出一个整数,表示可完成的最长滑雪长度。
5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
25
前置题目:0285
前置知识:递归
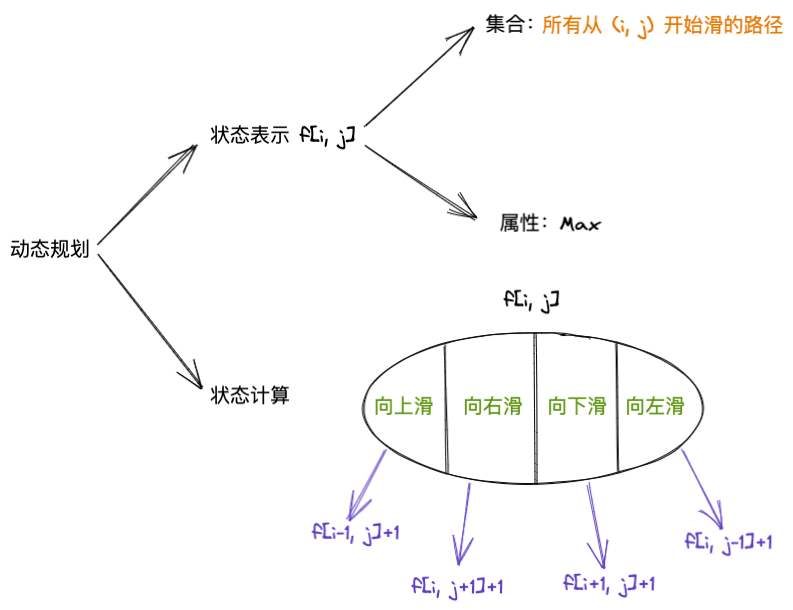
本题知识:动态规划-记忆化搜索
状态集合是从任意一个点为起点开始滑的所有状态,求这之中的最大值。 状态计算,已知起点了,下一步只有分解成四个方向。
f 二维数组初始化的时候最好统一赋值为 -1,防止误被认为已经被搜索过
记忆化搜索简单来说就是将已经计算过的数值保存下来,下次直接使用而不需重复计算。最简单的一个例子就是求斐波那切数列,如果不将前面的值计算后保存下来,后续递归计算的时候会重复计算好多次。
本题需要注意,如此分解方法不要构成循环。比如 a 需要通过 b 求解,b 需要通过 c 求解,c 需要通过 a 求解,这样无限循环永远也求不出答案。不过本题的要求满足了一个单调递减的条件 a > b,b > c 这样 c 不可能大于 a,就不可能构成环路,满足求解条件。