-
Notifications
You must be signed in to change notification settings - Fork 2.4k
Description
What version of OR-tools and what language are you using?
Version: 7.5.7466
Language: Python
Which solver are you using (e.g. CP-SAT, Routing Solver, GLOP, BOP, Gurobi)
Routing Solver
What operating system (Linux, Windows, ...) and version?
Linux 16.04 LTS
What did you do?
I am using the routing package to create optimized delivery routes for my work. One of the business constraints that I need to ensure is that enough vehicles will return from the AM delivery routes by a certain time to be ready to go for the PM routes. To do this, I added several dummy stops (one for each vehicle needed to return early), set time windows such that these dummies needed to be visited before the "return time", and manipulated the elements of the distance/time matrices such that there is no penalty for going from depot <--> dummy, the cost of going from customer -> dummy is the same as customer -> depot, and an "infinite" cost to go from dummy <--> dummy or dummy -> customer. This forces the dummy to be the last stop on the route before returning to the depot in a timely manner, and each truck can only visit one dummy max.
However, I found that implementing this constraint was causing the solver to fail without finding any solutions. The weird thing I noticed is that it would fail in scenarios where the solution to the unconstrained problem just happened to satisfy the constraints by chance. After doing some debugging, I found the difficulty comes in when trying to set the matrix elements to "infinity". As I have learned, ortools represents all internal calculations using 64-bit integers, so the largest value that can be used is MAX_INT = 2**63 - 1, which is more than enough for my purposes. Unfortunately, setting the distance/time from dummy -> customer to MAX_INT causes the solver to fail. Setting the distance/time from dummy <--> dummy to MAX_INT, however, works just fine. So it doesn't appear to be a problem with the value itself.
I have set up the problem such that the maximum distance/time matrix element values have both been normalized to the same value, let's call it PRECISION (I've typically been using values of 1e3 - 1e4 for this, even as high as 1e6 in the course of debugging). It turns out that by replacing MAX_INT with the "finite" value C * PRECISION (where C is some O(1) value) I can get the solver to start working again. However, because the distance from dummy -> customer is now comparable to the largest distance between customers, it is not guaranteed that the arc from dummy -> customer is forbidden anymore (and I have observed several cases where this does happen). Like I said before, in chance scenarios I have been able to get the unconstrained solution to satisfy the constrained problem, but using MAX_INT instead of C * PRECISION causes it to fail.
What did you expect to see
Expected solver to return solutions to the constrained problem (when the constrained problem is feasible).
What did you see instead?
Solver fails, even when unconstrained solutions to the problem happen to satisfy the constrained problem.
Anything else we should know about your project / environment
I have attempted to make a minimal reproduction of this issue below. Running this snippet with C = 25 works fine, but with C = 30 causes the solver to fail to find a route. I know setting the seed isn't guaranteed to create reproducible result across machines, but if you play around with it a bit you can probably reproduce the effect.
import time, re
from colorama import Fore, Back, Style
import numpy as np
from scipy.spatial.distance import pdist, squareform
from ortools.constraint_solver import pywrapcp, routing_enums_pb2
RNG_SEED = 42
NUM_STOPS = 200
NUM_DUMMIES = 3
NUM_VEHICLES = 7
PRECISION = 10_000
C = 25
def color_substr(string, substr, color):
start = getattr(Fore, color)
end = Fore.RESET
return re.sub(substr, start + substr + end, string)
def main():
np.random.seed(RNG_SEED)
# Generate location stops
locations = np.random.randn(NUM_STOPS + NUM_DUMMIES + 1, 2)
# Depot/dummies are located at (0, 0)
for i in [0] + list(range(-NUM_DUMMIES, 0)):
locations[i] = (0, 0)
# Set up routing manager/problem
manager = pywrapcp.RoutingIndexManager(len(locations), NUM_VEHICLES, 0)
routing = pywrapcp.RoutingModel(manager)
# Convert to distance matrix (with some added noise)
D = squareform(pdist(locations))
D += 0.1 * D.mean() * np.random.randn(*D.shape)
# Convert to integers
scale = PRECISION / D.max()
D = (scale * D).round().astype(int)
# Fix matrix elements between dummies and everyone else
dept_idx = [0]
cust_idx = slice(1, NUM_STOPS + 1)
dum_idx = slice(NUM_STOPS + 1, len(locations))
inf = 2 ** 63 - 1
D[dept_idx, dum_idx] = 0
D[cust_idx, dum_idx] = D[cust_idx, dept_idx]
D[dum_idx, dept_idx] = 0
D[dum_idx, dum_idx] = int(round(C * PRECISION))
D[dum_idx, cust_idx] = int(round(C * PRECISION))
# D[dum_idx, dum_idx] = inf
# D[dum_idx, cust_idx] = inf
D[np.eye(len(D)).astype(bool)] = 0
# Try another way?
# Set domain of stop following dummy to be depot only
# cust_idx = np.arange(1, NUM_STOPS + 1)
# dum_idx = np.arange(NUM_STOPS + 1, len(locations))
# dept_idx = manager.NodeToIndex(0)
# cust_idx = [manager.NodeToIndex(i) for i in cust_idx]
# dum_idx = [manager.NodeToIndex(i) for i in dum_idx]
# for d in dum_idx:
# n = routing.NextVar(d)
# # n.SetValues(NUM_VEHICLES * [dept_idx])
# n.RemoveValues(cust_idx)
# Set up distance callback
def dist_callback(from_index, to_index):
from_node = manager.IndexToNode(from_index)
to_node = manager.IndexToNode(to_index)
return int(D[from_node, to_node])
DIST_CALLBACK_IDX = routing.RegisterTransitCallback(dist_callback)
# Add cumulative distance variable
routing.AddDimension(
DIST_CALLBACK_IDX,
0, # no such thing as distance slack
int(scale * 100000000), # Max travel distance per vehicle
True, # Force start cumul to zero
"Distance", # Name of the dimension
)
# Add cumulative time variable proportional to distance
routing.AddDimension(
DIST_CALLBACK_IDX,
int(scale * 1000), # time slack
int(scale * 100000000), # Max travel distance per vehicle
False, # don't force start cumul to zero
"Time", # Name of the dimension
)
# Create some random time windows
MAX_TW = 100 * PRECISION
TW = np.random.uniform(size=(NUM_STOPS + NUM_DUMMIES + 1, 2))
TW = (MAX_TW * TW).round().astype(int)
TW.sort(axis=1) # make sure min < max
TW[0] = (0, MAX_TW) # depot is available anytime
TW[dum_idx] = (0, MAX_TW // 2) # dummies have to be visited by some cutoff
# Set TW constraints
time_dimension = routing.GetDimensionOrDie("Time")
for loc_idx, tw in enumerate(TW):
idx = manager.NodeToIndex(loc_idx)
time_dimension.CumulVar(idx).SetRange(int(tw[0]), int(tw[1]))
# Set objective
dist_dimension = routing.GetDimensionOrDie("Distance")
dist_dimension.SetSpanCostCoefficientForAllVehicles(1)
# Initiate solver
search_params = pywrapcp.DefaultRoutingSearchParameters()
search_params.time_limit.seconds = 15
tic = time.time()
solution = routing.SolveWithParameters(search_params)
toc = time.time()
# Print results
print(
[
"ROUTING NOT SOLVED",
"ROUTING SUCCESS",
"ROUTING FAIL",
"ROUTING FAIL TIMEOUT",
"ROUTING INVALID",
][routing.status()]
)
print(f"{toc-tic:.1f} sec elapsed")
stops = []
for route_nr in range(NUM_VEHICLES):
index = routing.Start(route_nr)
node_idx = manager.IndexToNode(index)
stops.append([node_idx])
while not routing.IsEnd(index):
prev_idx = index
index = solution.Value(routing.NextVar(index))
node_idx = manager.IndexToNode(index)
stops[-1].append(node_idx)
dept_idx = [0]
cust_idx = list(range(1, NUM_STOPS + 1))
dum_idx = list(range(NUM_STOPS + 1, len(locations)))
print("Depot:", dept_idx)
print("Customers:", cust_idx)
print("Dummies:", Fore.RED, dum_idx, Fore.RESET)
print("Routes:")
for i, route in enumerate(stops):
for idx in dum_idx:
route = color_substr(str(route), str(idx), "RED")
print(f"\t{i}: {route}")
if __name__ == "__main__":
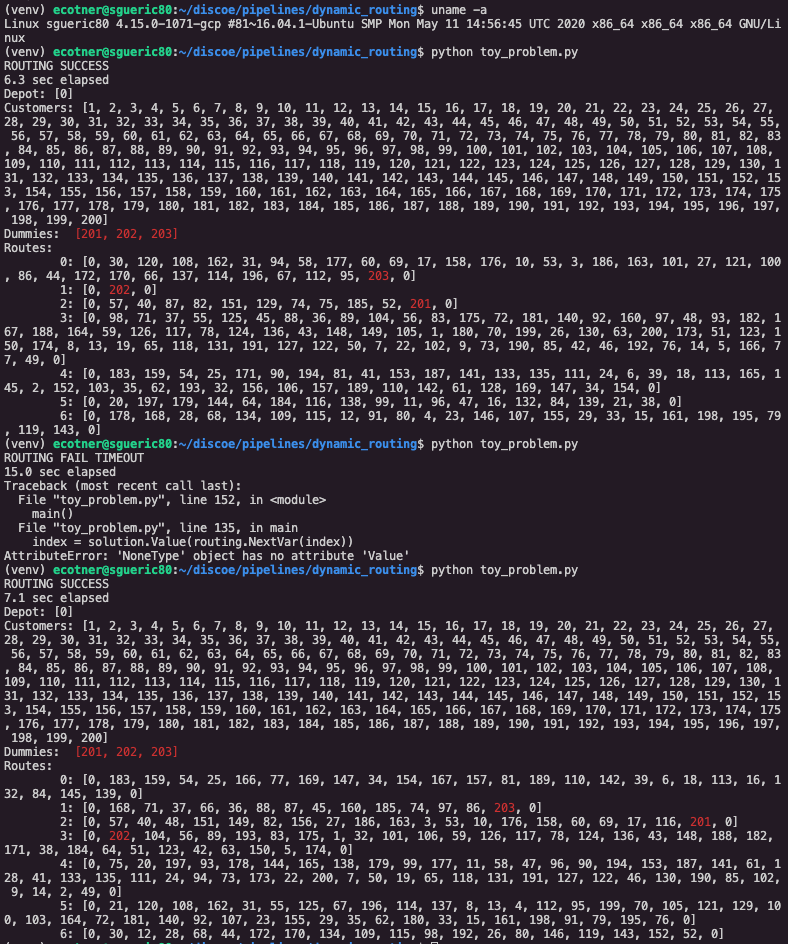
main()Here is a screenshot of my terminal output after running the script three times for the values C = 25, 30, 5 (in that order). You can see the dummy stops (in red) are at the end of the route when C=25, the solver fails for C=30, and the desired constraint is not satisfied when C = 5 (one of the dummies is the first stop on route 3, not last). The values I use for C in my full problem need to be much closer to 1, otherwise the solver fails.
My initial thoughts on this are
- I'm doing something horribly wrong
- The first solution heuristic is not appropriate for these kinds of constraints
- There is a bug in
ortools' solver
Hoping someone could help me out!