Minimize steps necessary to accomplish semi implicit Euler interpolation

[dbismut]

Description

Performance

This PR tries to implement indications given in this comment, with dt being related to the natural frequency (here 300/naturalFrequency) rather than always being 1ms, thus reducing the number of steps necessary to compute each frame.

Observation
In my observations, I've noticed slightly different behaviors of the springs when applying this change (usually the springs feel slightly faster). I might be doing something wrong.

Possible improvements
Here natural frequency is computed on each frame, although being a constant. It could be calculated only when tension or mass change.

Bounce behavior on clamp

Again, as @mtiller suggested, clamp could behave like a bouncing ball. This PR allows config.clamp to be a number, treated as the coefficient of restitution. Below is an animation of config.clamp = 2.

This PR also computes lastVelocity and lastTime for easing and decay.

[aleclarson]

Nice work! 🎉

Run git pull --rebase to sync up with v9 again, please.

[aleclarson]

Why is * (2 * Math.PI) needed?

[dbismut]

Ok, so I asked help around to sort this out and just pushed new code:

const w0 = Math.sqrt(config.tension! / config.mass!)
const dt = 100 / w0
const numSteps = Math.ceil(deltaTime / dt)

for (let n = 0; n < numSteps; ++n) {
  const springForce = -config.tension! * (position - to)
  const dampingForce = -config.friction! * (velocity * 1000)
  const acceleration = (springForce + dampingForce) / config.mass!
  velocity = velocity + (acceleration * dt) / (1000 * 1000) // expressed in ms
  position = position + velocity * dt
}

Disclaimer: the following is only my understanding

I think I was confused by the term natural frequency, which isn't what w0 is. The correct term for w0 is angular frequency.

The stability criterion from the article, equation 23 page 23 @mtiller was referring to is valid only for undamped harmonic oscillator. I suspect that the right formula for damped harmonic oscillator is actually dt < Math.sqrt(2) / w0 instead of dt < 2 / w0.

The stability criterion makes sure your oscillator is stable (meaning it will get to its destination eventually), but there will be a margin of error, and the closer you get to the stability limit, the more the spring will behave erratically compared to the analytical solution.

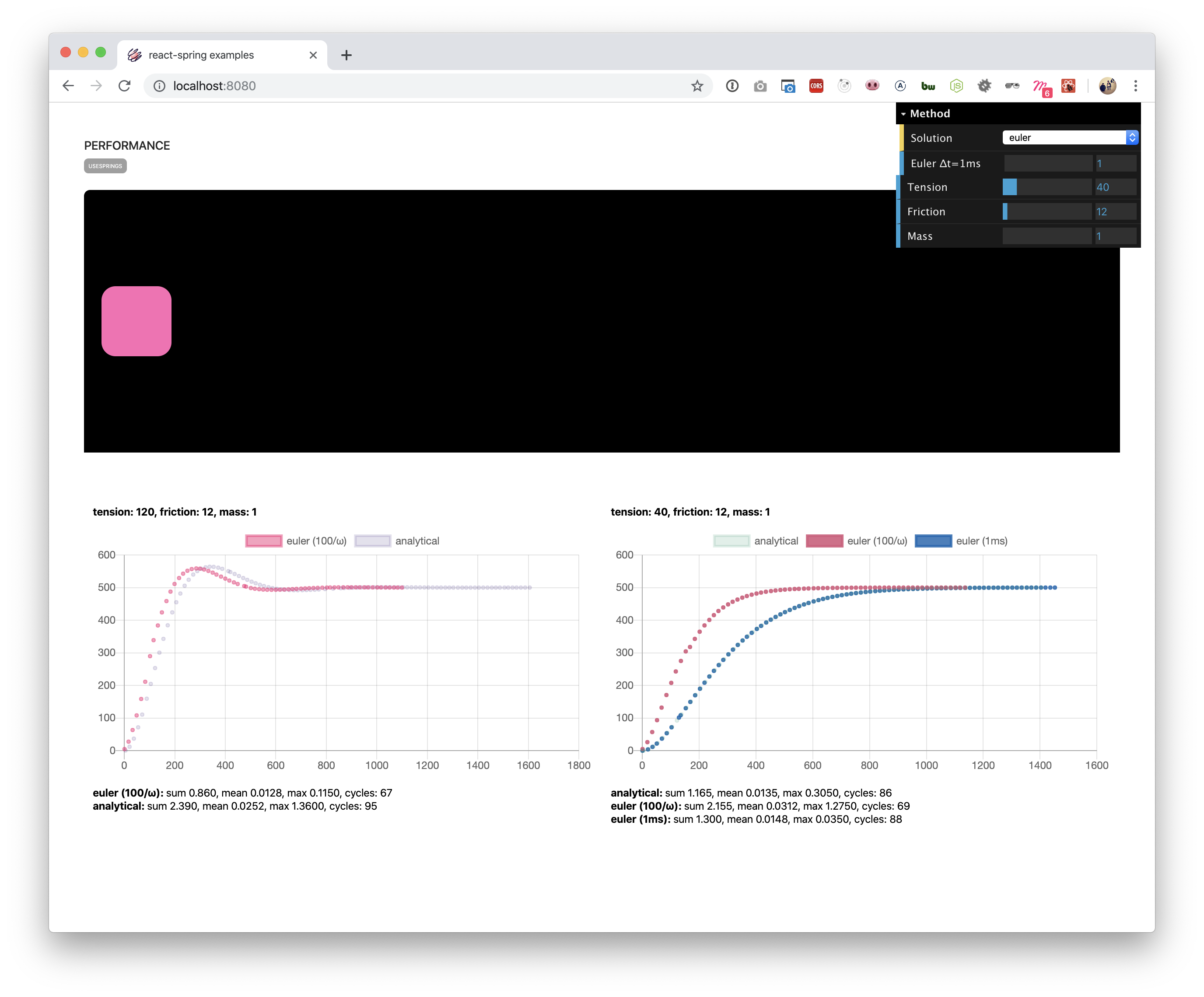
Here, I've set dt = 0.1 / w (actually dt = 100/w as these are ms), and it seems to behave pretty close to when dt was 1ms. My observation is that we move from 10-20 steps to just 2-3 steps in average for the following config: config: { tension: 120, friction: 12, mass: 1 }.

[aleclarson]

Can you open a PR on react-spring-examples for the example in that gif?

Aim it at pmndrs/react-spring-examples#10

[dbismut]

Run git pull --rebase to sync up with v9 again, please.
Here's the steps I made to synced the forked branch:

git fetch upstream  
git checkout v9
git merge upstream/v9

And then I rebased this branch onto v9 via Github desktop. Again apologies if this is not the way to go, but git pull --rebase didn't do anything.

[dbismut]

Can you open a PR on react-spring-examples for the example in that gif?

Done! pmndrs/react-spring-examples#21

[aleclarson]

but git pull --rebase didn't do anything.

Whoops, I meant git pull --rebase v9 :P

[aleclarson]

FYI: I force pushed to sync with v9 branch.

I'll test out this PR in ~24 hours. 👍

[dbismut]

@aleclarson I’m currently working on an example that will let you change the steps, alternate between analytical and Euler algorithm, plot the results on a graph, and make performance analysis. Obviously this would use a modified version of this PR, but I’d love to publish this somewhere online for you to have a look.

[aleclarson]

Nice! I'll wait until then to try this PR out. Just setup a webpack repo with the example that uses your fork. That should be good enough for now. 👍

[dbismut]

@aleclarson Just finished, not sure how easy this is to set up for you but:

• here is the react-spring fork: https://github.com/dbismut/react-spring/tree/feat/performance
• here is the react-spring-examples fork: https://github.com/dbismut/react-use-gesture-examples/tree/v9-performance

It should look like this:

I've made some tests and I'm not sure about the conclusions just yet. It looks like increasing dt has some severe precision impact on low tension springs. Performance is also pretty erratic to measure, that might need some improvements.

[dbismut]

@aleclarson some of our commits conflicted as I was trying to use raf step and therefore use a common step for all animated values in the frame loop. I've asked @drcmda if it was ok but he told me that react-three-fiber calls updates manually and that might interfere with this idea. I'm waiting for him to get back to me.

As far as I can see, it seems to work properly.

[aleclarson]

some of our commits conflicted

FYI: Using git pull --rebase instead of git pull should let you fix the conflicts without introducing a merge commit. Not a huge deal, since I'll be squashing this before merging, but just wanted to let you know ;)

[dbismut]

I'm using Github desktop (roast me)

[dbismut]

What it does

Today, precision is used to determine when to rest the spring, ie when velocity is close enough to 0 and current position is close enough to its target position. The higher the precision, the longer the spring comes to rest.

Precision is set by default to 0.005.

However, animating opacity requires usually more precision than animating translate. In that case, 0.005 is fine for opacity (if you're animating opacity from 0 to 1, the spring would come to rest is when its position is higher than 0.995 and smaller than 1.005). However, animating a translate from 0 to 100 would rest when the position is higher than 99.995 and smaller than 100.005. This amount of precision is probably exaggerated for a movement of that kind.

This commit makes it so that the precision of the animation would by default depend on the magnitude of the displacement. When animating from 0 to 1 the default precision would be 0.001. When animating from 0 to 100, the default precision would be 0.1.

Why it matters

The commit tries to rest the spring when no more movement is perceivable by the user. Currently and in some situations where the displacement is significant, onRest would fire with a noticeable delay vs the moment where the user thinks the spring is at rest. This commit aims at reducing this perception.

By the numbers

Animating a spring with config: { tension: 120, friction: 12, mass: 1 } from -250 to 250 would originally take ~1450ms before onRest was fired. With this commit, it only takes ~820ms.

[aleclarson]

I think this is ready to squash and merge.

@dbismut @drcmda WDYT?

[dbismut]

I think this is ready to squash and merge.

I'm not sure just yet: the step chosen here 0.05 / ω can have significant impact on precision as you can see from the graph below:

I'm trying to understand how to evaluate the marginal error and compute a step formula that would result in better precision. If we want to leave this aside for later, we should probably stick to step = 1ms for now.

Should we also amend tests?

[dbismut]

@aleclarson any reason why this.lastVelocity is reset to null and not undefined? null makes the test below not behave as it should:

 velocity = animated.lastVelocity !== void 0 ? animated.lastVelocity : v0

[aleclarson]

That was a mistake, but my local clone has animated.lastVelocity == null to account for that change.

[dbismut]

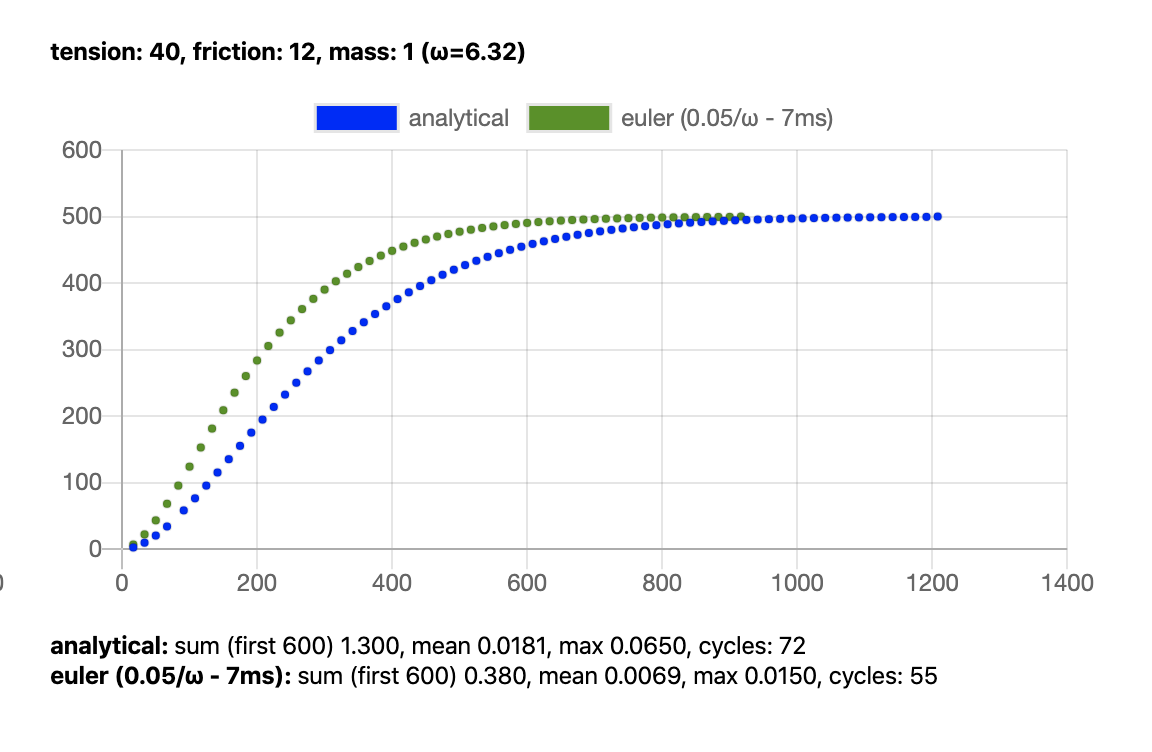
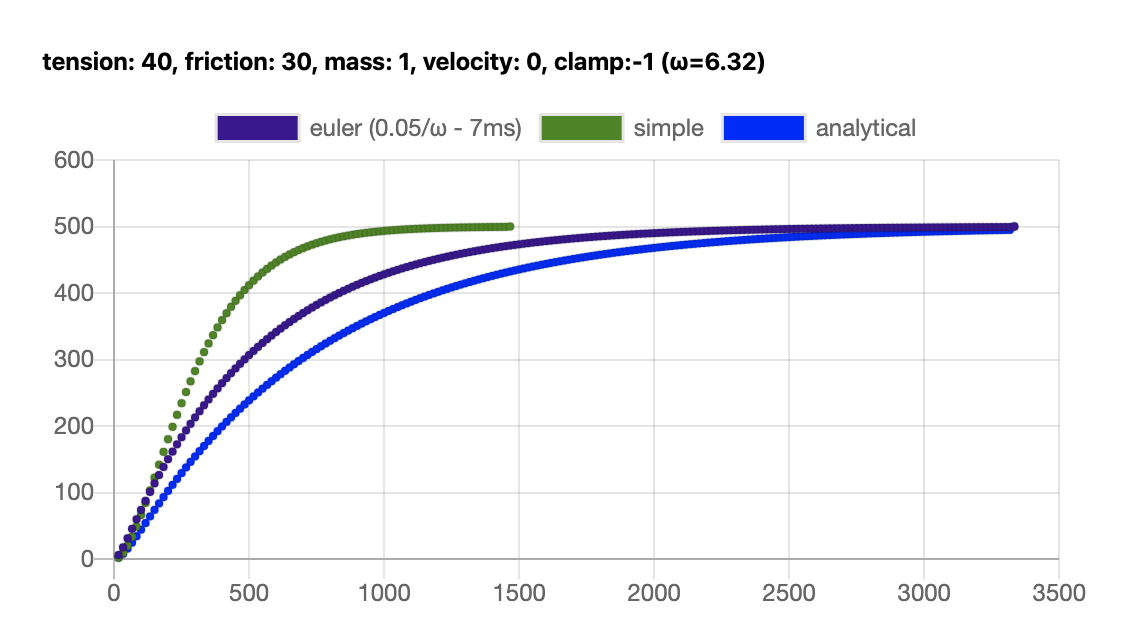
FWIW, I've updated the precision simulator to enable clamp and initial velocity. The simple algorithm is a simplified version of the analytical algorithm (used by popmotion), that isn't really true to underdamped systems but actually has a better behavior. I've also fixed the clamping on analytical solutions which are now closer to being candidates to replacing Semi Implicit Euler.

https://spring-perf.surge.sh/

Example with an underdamped oscillator:

[mtiller]

A few comments as I'm trying to catch up here.

First, I didn't quite follow the @dbismut means by analytical. But let me add an observation and he can comment on whether this is what he was doing. First, let me introduce some terminology:

With a spring, we can talk about the "unstretched length" of the spring. This is the natural length of a spring. Think of a physical spring. It has a natural length when nobody is pushing or pulling it. That is the unstretched length. Normally, a spring has a spring constant (in SI units, that would be Newtons/meter). The force generated by the spring is normally F = k(x-x_u) where x is the length of the spring and x_u is the unstretched length of the spring. So when they are equal, the spring transmits no force.

Now here is the thing that @dbismut's comments about analytical got me thinking about. Let's say that you have a spring where x is 10 and x_u is 5 and (and, of course, you have some mass and some damping), then you actually know precisely where the spring is going to go. You don't need to integrate, this is a linear system. The entire trajectory is known out to infinity from just a single equation. The equation will basically be of the form:

x = (x_0-x_u)*e^-(a*(t-t_0))*sin(w_0*(t-t_0))+x_u

...where x_0 is the initial displacement of the spring, a is the time constant of the decay, w_0 is the natural frequency, t is the current time, t_0 is the time that the motion started and x_u is the unstretched length. If you look closely, you see that the first term there will got to zero for any a>0. At the point where the motion starts, all you actually need to compute is x_0, a and w_0 (you already know x_u, that is the to value), make a note of t0 and then every time you get a request for animation frame, just plug t into this equation and it will given you back x.

Now, there is one complication. What happens if the to value changes? Presumably, this gets cascaded down as a result of a props change. Well, no problem. Just start over. This happens much less frequently than requests for animation. The x_0 will just be the current value of x from the old equation, a and w_0 can be easily recomputed (in my opinion, these should actually be the props) and x_u is just the latest to value. Just update t_0 to the time when the props where changed and you have an updated, closed-form solution for the trajectory.

This should be pretty much as fast as is possible. No more need for every RAF to run the integrator to catch up to current time. Just compute the closed-form solution for what the current position should be. No need to compute velocities at all.

Note that you can also easily resolve the issue of when to "clamp" the spring. To be honest, if you put this in place I'm not even sure if there would be a performance issue with just continuing to use the equation indefinitely. But if you were worried about it, just find out when the amplitude of the displacement ends up being some arbitrary fraction of the initial displacement. For example, if you want to stop computing things once you get to 1% of the original displacement, you just need to solve this equation for t_f:

e^-a(t_f-t_0)*=0.01

...or...

t_f = -ln(0.01)/a + t_0

That would then be the magic time at which you could just clamp the position to be to.

Now I tried to skim through the comments to understand the latest thinking. Perhaps this is exactly what @dbismut is doing or proposing. Sorry if I'm just lecturing on something every already realized. But if you aren't doing it this way, I think this would be the absolute optimal way to proceed in terms of both performance and accuracy.

My apologies that all these comments come so late and if I'm somehow missing something important rendering all this commentary totally irrelevant. I'll try to stay more plugged in to these comments but trust me when I say lots of other stuff in my inbox is currently feeling neglected.

P.S. - At some point, I picked up the code and actually tried to work on the loop in question. But every time I messed with it, the tests failed. So I wasn't quite sure how to put together a PR around this. How are you guys testing?

[dbismut]

Hey @mtiller, great to read you here, all this is because of you in the first place! Before all, I would like to apologize for having mentioned your handle far too much, I'm amazed you were able to navigate through all the threads and make sense of them.

Here are some highlights of where I'm at.

Minimizing steps for semi implicit Euler

Minimizing steps for SIE is precisely the object of this PR that has been greatly inspired by your post. The whole objective was to optimize the algorithm cpu-wise and this objective led me to consider analytical solutions — I was using the analytical term by contrast with numerical (Euler, RK4), I think I read that somewhere.

I tried using a step correlated to the stability coefficient 2/ω (which I believe is only true to undamped oscillators): this PR currently uses a step = 0.05/ω but I quickly ran into perceptible accuracy issues with certain spring configurations. This is why I built a spring algorithm comparison tool and a performance benchmark tool which you'll find below.

EDIT: the question I have is: is there a way to measure the error generated by the length of the step? The idea would be to find the maximum acceptable step.

Analytical solution (Apple-like)

What you mentioned in your post above is what I figured out after a few days looking at different spring libraries, which all mention Apple for being the source of this equation, but I realized this is just math after all. Below are two implementations of the equation you mentioned, both claim to be inspired from CASpringAnimation in iOS.

Whenever the destination value to changes, I'm resetting the animation elapsedTime, setting the initial velocity v_0 to the last computed velocity of the spring, and setting the x_0 origin to the current position of the spring.

I'm still using difference between the current position and the destination target in addition to velocity being close to zero to evaluate when resting the spring, is there any benefit in using t_f = -ln(0.01)/a + t_0?

What made me pursue the numerical route is that I thought that with a sufficiently large step the iteration on each RAF frame might be faster than computing exponentials and trigonometric functions.

Wobble Analytical

This is stolen from the library wobble, and I guess is the most complete equation, differentiating under damped, critically damped and over damped systems.

Simplified Analytical

This is a simplified version of the above equation, used by the library popmotion, working well for underdamped springs (but with a different behavior for overdamped springs, you can check that using the tools below). It also uses a numerical approximation of the velocity instead of the executing the derivative of the position equation (which I suspect is faster).

In my opinion, this is the best candidate in replacing the current algorithm.

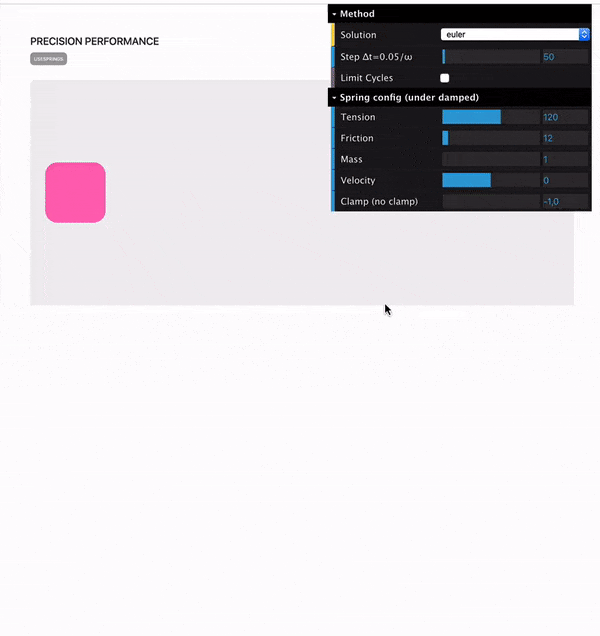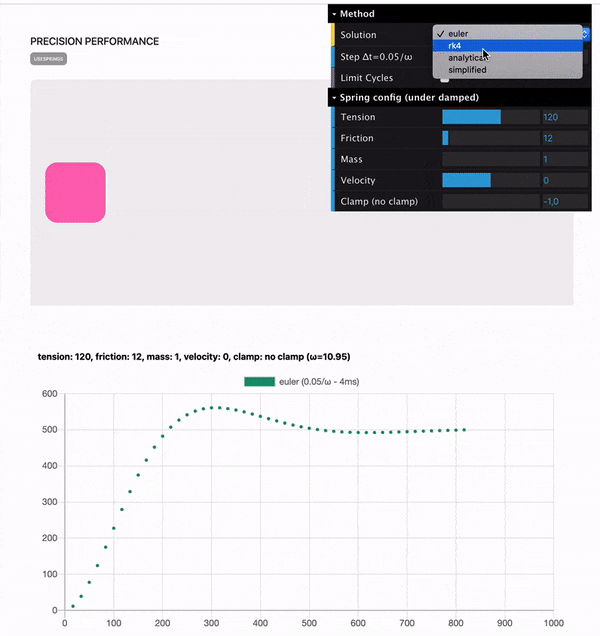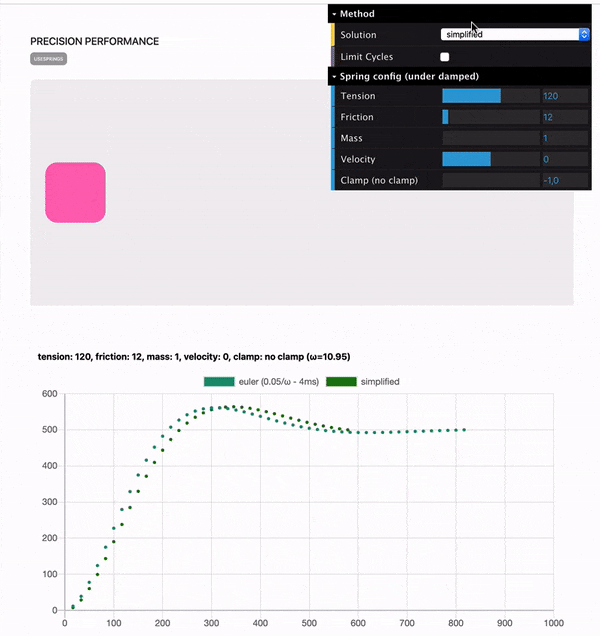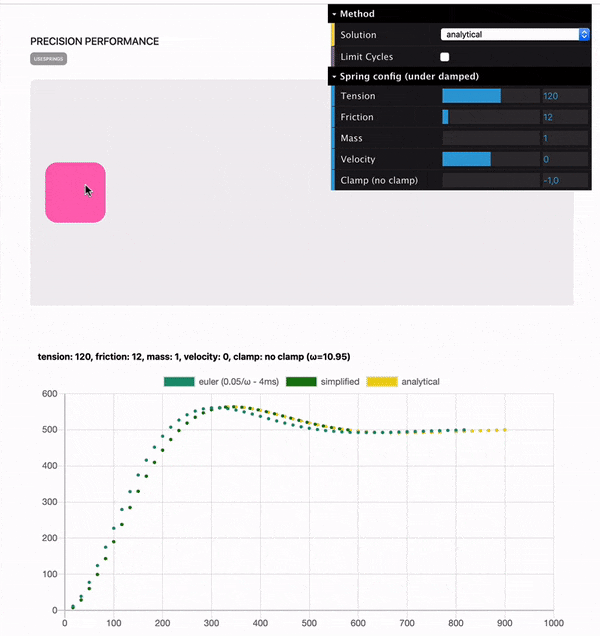
After some further testing, useTrail doesn't work properly with analytical solutions. Also performance seems smoother with semi implicit Euler when animating lots of springs 🤯

Benchmarking tools

As I mentioned, I built two tools to be able to evaluate both accuracy and cpu performance.

Precision benchmark

This one is available at https://spring-perf.surge.sh/

It allows you to visualise the curve of the spring movement on a chart. To initiate a precision chart, just click on the pink square. You can also drag it and it will follow your cursor based on the config set in the GUI in the top right.

It also does some very poor performance analysis that I wouldn't look at too much.

Here are the available options from the GUI:

• Solution: solving algorithm. Euler is semi implicit Euler.
• Step: iteration step. When <= 20 it is used as milliseconds, when >20 it is used as a fraction of the angular frequency step * 0.001 / ω
• Limit Cycles: will limit the movement to the first 30 cycles. This is useful when testing an undamped (frictionless) oscillator which never comes to rest.
• Tension, friction, mass: characteristics of the oscillator
• Velocity: initial velocity of the object
• Clamp: whether to clamp the movement (-1 is no clamping by default, other values are used as restitution coefficient).

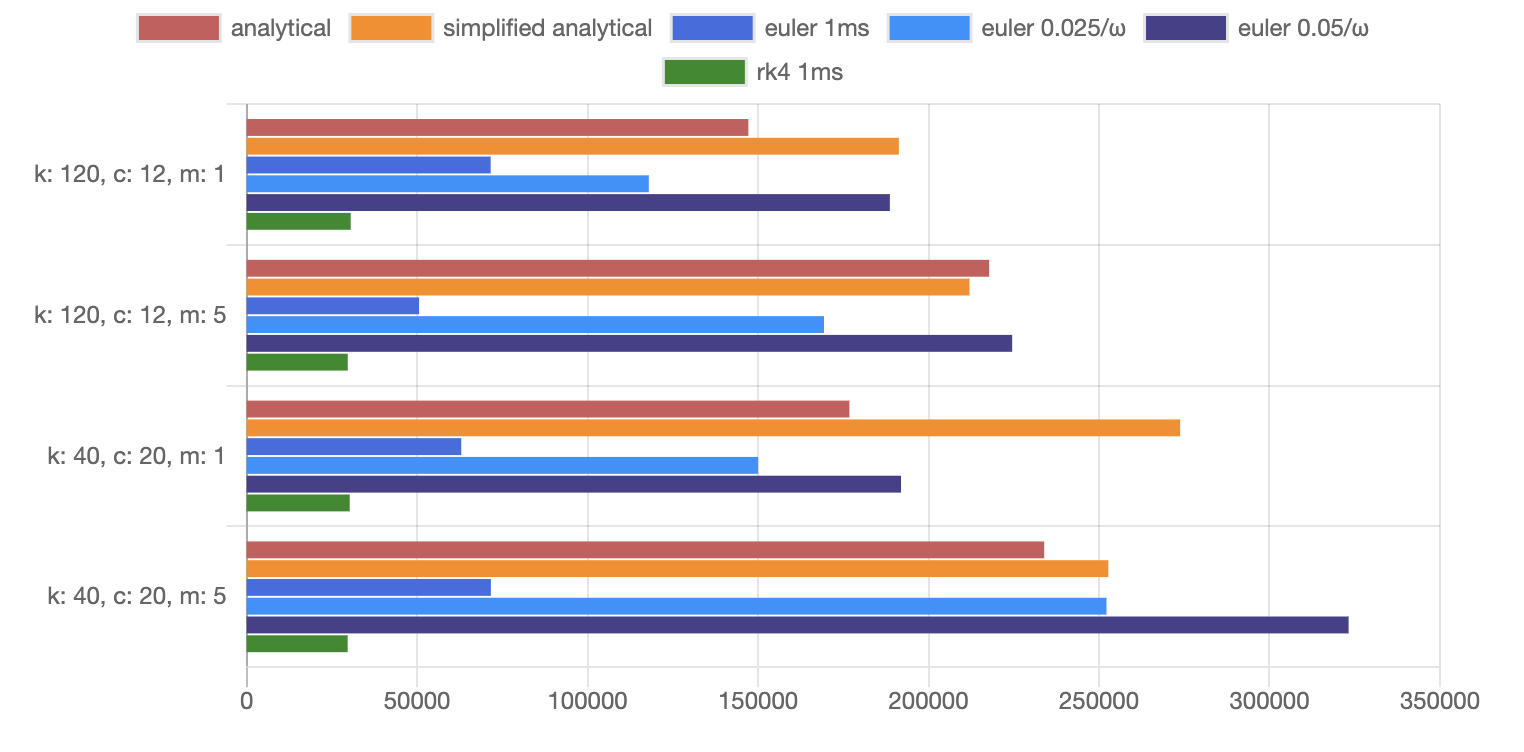
Performance benchmark

This benchmark is available at https://66tpc.csb.app/ and the source code is on codesandbox.

Here RAF is replaced with a while(!finished) loop to compare raw performance of the different algorithms. Results may vary depending on the computer and browser you're using. Here are my results on Chrome, MacBook Pro 2017:

How to test

If you want to iterate from there and test different algorithms + having the same precision benchmark tool explained above, I suggest you use the forks I created:

If so, you should do the following:

$ git clone https://github.com/dbismut/react-spring.git -b feat/performance
$ cd react-spring
$ yarn
$ git clone https://github.com/dbismut/react-use-gesture-examples.git -b v9-performance examples
$ cd examples
$ yarn
$ yarn start

The examples will use the local version of react-spring.

[aleclarson]

Merged into #808